It looks as though the first force is
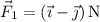
The second force acts in the direction of
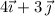 . Normalize this direction vector to make it have length 1:
. Normalize this direction vector to make it have length 1:
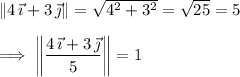
Then the second force is

The resultant force is
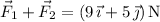
Assuming the particle moves 2 m in the same direction as the resultant force, the work perfomed on the particle by it is
