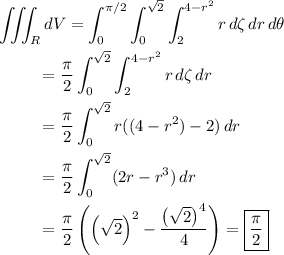In Cartesian coordinates, the region (call it
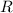 ) is the set
) is the set
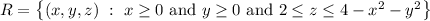
In the plane
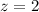 , we have
, we have
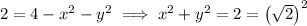
which is a circle with radius
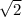 . Then we can better describe the solid by
. Then we can better describe the solid by
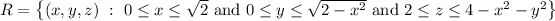
so that the volume is
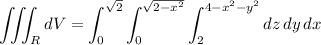
While doable, it's easier to compute the volume in cylindrical coordinates.
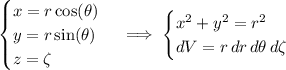
Then we can describe
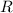 in cylindrical coordinates by
in cylindrical coordinates by
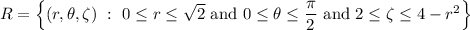
so that the volume is