Answer:
See explanation below
Explanation:
If the base of a radical exponent is the same then the following properties hole and x≠ 0
![\sqrt[n]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/82umi5h7pf7ttup974ahitbbdz5w1ee0u3.png) =
=
 Rule 1
Rule 1
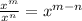 Rule 2
Rule 2
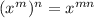 Rule 3
Rule 3
The numerator in the expression is
![\sqrt[3]{x^2y^5} =(x^2)^(1)/(3) (y^5)^(1)/(3) = x^(2)/(3)} . y ^ (5)/(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/bynaj81h3fmyd32uidt8t5embttfsormju.png) Using rules 1 and 3
Using rules 1 and 3
The denominator is
![\sqrt[4]{x^3y^4} =(x^3)^(1)/(4) (y^4)^(1)/(4) = x^(3)/(4)} . y ^ 1}](https://img.qammunity.org/2023/formulas/mathematics/high-school/zn2baag01cwynzwuklgli8ryc13n74v1m5.png) Using rules 1 and 3
Using rules 1 and 3
Therefore the original expression in exponent form is
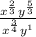
Using rule 2 we get the final expression as
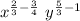
2/3 - 3/4 = 8/12 - 9/12 = -1/2
5/3 - 1 = 5/3 - 3/3 = 2/3
So the final expression is
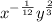
Proved