Question

An object with an acceleration of -6.65m/s squared moves from a rate of 78m/s to 2 m/s. How far will the object have traveled during that interval?​

Answer 1

Approximately
`4.6 * 10^(2)\; \rm m`.

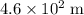Step-by-step explanation:

The acceleration of this object is constant. Hence, the SUVAT equation would apply to the motion of this object. Since the duration of this acceleration is not given, apply the SUVAT equation that does not include time.

• Let
  `u` denote the initial velocity of this object.
• Let
  `v` denote the velocity of this object after the acceleration.
• Let
  `a` denote the acceleration of this object.
• Let
  `x` denote the displacement of this object.

`v^(2) - u^(2) = 2\, a\, x`.

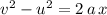Rearrange this equation to find an expression for displacement,
`x`:

`\begin{aligned}x &= (v^(2) - u^(2))/(2\, a)\end{aligned}`.

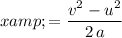In this question, it is given that the initial velocity is
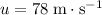`u = 78\; \rm m\cdot s^(-1)`, the velocity after acceleration is
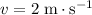`v = 2\; \rm m\cdot s^(-1)`, and the acceleration is
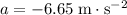`a = -6.65\; \rm m\cdot s^(-2)`. Evaluate the expression above to find the displacement of this object:

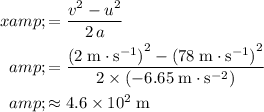`\begin{aligned}x &= (v^(2) - u^(2))/(2\, a) \\ &= \frac{{(2\; \rm m\cdot s^(-1))}^(2) - {(78\; \rm m\cdot s^(-1))}^(2)}{2 * (-6.65\; \rm m\cdot s^(-2))} \\ & \approx 4.6 * 10^(2)\; \rm m\end{aligned}`.