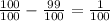Question

Hey guys please help? Trigonometry

So, the task is: find cos a, if:

1) sin a = (3√11)/10, a ∈ (0; π/2)

2) sin a = (3√11)/10, a ∈ (π/2; π)


Could someone please explain how to solve it? I can't figure out what difference a ∈ (0; π/2) and a ∈ (π/2; π) make in the way I have to solve it mmh... I'll pin my attempt to do the first one (failed for some reason)

Answer 1

Explanation:

a ∈ (0; π/2) here means that our angle, a must lie between 0 and pi/2, exclusive.

So this mean our angle must be in between 0 and pi/2, but can not be neither 0 and pi/2.

Here we have

`\sin( \alpha ) = (3 √(11) )/(10)`

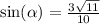
We must find cos.

Using the Pythagorean theorem

`( \sin( \alpha ) ) {}^(2) + ( \cos( \alpha ) ) {}^(2) = 1`

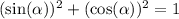
It is mostly notated as this,

`\sin {}^(2) ( \alpha ) + \cos {}^(2) ( \alpha ) = 1`

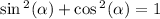
But they mean the same thing, we know

`\sin( \alpha ) = (3 √(11) )/(10)`

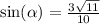
So we plug that in for sin a.

`( (3 √(11) )/(10) ) {}^(2) + \cos {}^(2) ( \alpha ) = 1`

`(99)/(100) + \cos {}^(2) ( \alpha ) = 1`

`\cos {}^(2) ( \alpha ) = (100)/(100) - (99)/(100)`

`\cos {}^(2) ( \alpha ) = (1)/(100)`

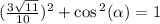
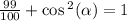
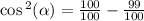
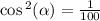
Since cos is Positve over the interval (0; π/2), we take the positive or principal square root.

`\cos( \alpha ) = (1)/(10)`

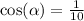
2. We would get the same work for the second part, the only difference is that cosine is negative over the interval

(π/2, π)

So the answer for 2 is

`\cos( \alpha ) = - (1)/(10)`

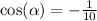
Disclaimer: Your work you did was correct, just remember for fractions like

`1 - (99)/(100)`

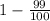
Convert 1 into a fraction that has a denominator of 100.

`(100)/(100) - (99)/(100) = (1)/(100)`