Answer:
there are 186 children, 93 adults and 44 students.
Explanation:
there are 323 seats;
there is 2 children for 1 adult. rather the ratio between children and adults is 2:1
we can take the number of students to be y;
if we take the number of adults to be x then number of children will be 2x.
so in genral
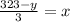
this means if you substract the number of students then you are left with only children and adults and we know the are x and 2x that is 3x. so if we divide 323-y by 3 we get x or rather the number of adults.
another inequality;
2354$ -7$*y = 12x+10x
we know the price for a student is 7$ so if we minus that from the total we get the total ticket price from only adults and childrens.
we know if there are x adults then the total adult ticket price is 12x. we know there are twice the number of adults, so the total ticket price for children is 5x*2 or 10x. this is the above inequality.
we have now two equations;
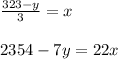
we change the form of 1st one.
323-y = 3x
now multiply 7 on both sides we get'
2261 -7y = 21x
if we substract this from the second equation we can find theh value of x. which will be 93.
number of adults = 93, number of children = 93x3 =186 and put the value of x in one of the equation to find y, which is 44.