According to the problem, we have a 0.200 M solution of a weak acid HA that is 9.4% ionized. To find the Ka (acid dissociation constant) for HA, we can use the percent ionization formula:
From this formula, we know that [H+] (the concentration of hydrogen ions) is equal to 9.4% of [HA]initial, and [HA]initial is equal to the initial concentration of the weak acid, which is 0.200 M. Solving for [H+], we get:
Now we can use the equation for Ka:
We don't know the concentration of the conjugate base (A-) at this point, but we can assume that it is equal to [H+] because the weak acid is only slightly ionized. Therefore, we can substitute [A-] = [H+] = 0.0188 M into the equation and solve for Ka:
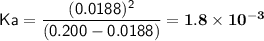
So the answer is
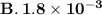 .
.
I hope this helps!