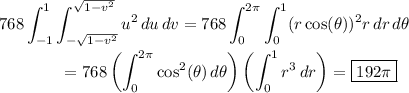Question

Use the given transformation x=4u, y=3v to evaluate the integral. ∬r4x2 da, where r is the region bounded by the ellipse x216 y29=1

Answer 1

The Jacobian for this transformation is

`J = \begin{bmatrix} x_u & x_v \\ y_u & y_v \end{bmatrix} = \begin{bmatrix} 4 & 0 \\ 0 & 3 \end{bmatrix}`

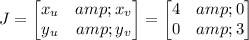
with determinant
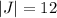`|J| = 12`, hence the area element becomes

`dA = dx\,dy = 12 \, du\,dv`

Then the integral becomes

`\displaystyle \iint_(R') 4x^2 \, dA = 768 \iint_R u^2 \, du \, dv`

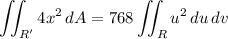
where
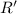`R'` is the unit circle,

`(x^2)/(16) + \frac{y^2}9 = ((4u^2))/(16) + \frac{(3v)^2}9 = u^2 + v^2 = 1`

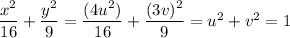
so that

`\displaystyle 768 \iint_R u^2 \, du \, dv = 768 \int_(-1)^1 \int_(-√(1-v^2))^(√(1-v^2)) u^2 \, du \, dv`

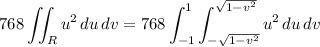
Now you could evaluate the integral as-is, but it's really much easier to do if we convert to polar coordinates.

`\begin{cases} u = r\cos(\theta) \\ v = r\sin(\theta) \\ u^2+v^2 = r^2\\ du\,dv = r\,dr\,d\theta\end{cases}`

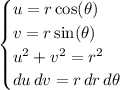
Then

`\displaystyle 768 \int_(-1)^1 \int_(-√(1-v^2))^(√(1-v^2)) u^2\,du\,dv = 768 \int_0^(2\pi) \int_0^1 (r\cos(\theta))^2 r\,dr\,d\theta \\\\ ~~~~~~~~~~~~ = 768 \left(\int_0^(2\pi) \cos^2(\theta)\,d\theta\right) \left(\int_0^1 r^3\,dr\right) = \boxed{192\pi}`