Answer:
120
Explanation:
We have 5 digits that can be used to create different 5 digit numbers. We are also not allowed to repeat any numbers. Let's say we have 5 boxes to put the 5 numbers in.
Box 1
Box 2
Box 3
Box 4
Box 5
In the first box, we have 5 different choices. Since we aren't allowed to repeat any digits, the second box only has 4 different choices. And so on...
Box 1 --> 5 choices
Box 2 --> 4 choices
Box 3 --> 3 choices
Box 4 --> 2 choices
Box 5 --> 1 choice
Therefore the amount of 5 digit numbers that can be created is:
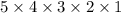 or 5 factorial (a factorial is all the product of all the positive integers equal to and less than the number), which is equivalent to:
or 5 factorial (a factorial is all the product of all the positive integers equal to and less than the number), which is equivalent to:
120 5-digit numbers