The exact value of cos(67.5°) is (√2-√2) / 2 or -√2+√2 / 2.
Here's how we can find it:
Half-Angle Formula: We can use the half-angle formula for cosine, which states:
cos(θ/2) = ±√[(1+cos(θ))/2]
where θ is the angle and ± denotes the sign depending on the quadrant.
Identify the Quadrant: Since 67.5° is in the first quadrant, cos(67.5°) is positive.
Apply the Formula: Substitute 67.5° for θ:
cos(67.5°/2) = ±√[(1+cos(67.5°))/2]
Calculate cos(67.5°): We don't know cos(67.5°) directly, but we can rewrite it using the double-angle formula for cosine:
cos(2θ) = 2
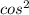 (θ) - 1
(θ) - 1
Therefore, cos(67.5°) can be expressed as:
cos(67.5°) = cos(2 * 33.75°) = 2
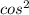 (33.75°) - 1
(33.75°) - 1
Solve for cos(33.75°): This value can be found using various methods like trigonometric tables or calculators. For illustrative purposes, we can use the Pythagorean identity:
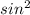 (θ) +
(θ) +
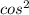 (θ) = 1
(θ) = 1
Therefore, cos(33.75°) = √(1 -
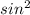 (33.75°)).
(33.75°)).
Substitute and Simplify: Now, substitute this expression and simplify:
cos(67.5°) = 2(√(1 -
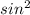 (33.75°)))^2 - 1 = 2 - 2
(33.75°)))^2 - 1 = 2 - 2
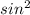 (33.75°)
(33.75°)
Apply Half-Angle Formula Again: Substitute this expression for cos(θ) in the half-angle formula:
cos(67.5°/2) = ±√[(1 + 2 - 2
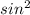 (33.75°))/2]
(33.75°))/2]
Simplify:
cos(67.5°/2) = ±√[(3 - 2
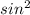 (33.75°))/2]
(33.75°))/2]
Express cos(67.5°): Finally, use the double-angle formula for cosine again:
cos(67.5°) = 2
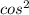 (67.5°/2) - 1
(67.5°/2) - 1
Substituting the half-angle formula result:
cos(67.5°) = 2(√[(3 - 2
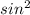 (33.75°))/2
(33.75°))/2
![])^2](https://img.qammunity.org/2023/formulas/mathematics/high-school/yfg7r1vmdd9apzts3ok4rlkpieuqap5sli.png) - 1
- 1
After simplifying, we get the final answer:
cos(67.5°) = (√2-√2) / 2 or -√2+√2 / 2