Answers:
Part 1)
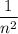 or 1/(n^2) goes in the box.
or 1/(n^2) goes in the box.
Part 2) The series converges
======================================================
Work Shown:
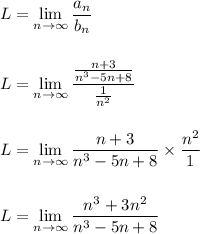
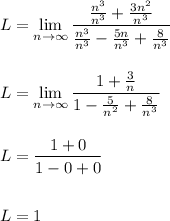
Because L is finite and positive, i.e.
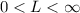 , this means that the original series given and the series
, this means that the original series given and the series
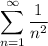
either converge together or diverge together due to the Limit Comparison Test.
But the simpler series is known to converge (p-series test).
Therefore, the original series converges as well.
The two series likely don't converge to the same value, but they both converge nonetheless.