Explanation:
So, there is something known as a removable discontinuity, and it's essentially where you can define f(x) using the most simplified fraction, where you could normally not define f(x).
So we have the following equation:

As you may know, we cannot divide a number by the value of zero. When the denominator is equal to zero, on the graph this will appear as a vertical asymptote, where x approaches the value that makes the denominator zero, but never actually reaches it.
If you look at each denominator, you can set them equal to zero to find the vertical asymptotes
x+1 = 0
x=-1
There should be a vertical asymptote at x=-1, since it would make two of the denominators equal to -1, but let's divide the two fractions first.
Original Equation

Keep, change, flip

Multiply the two fractions
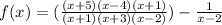
Notice how the x+1 is in the numerator and fraction? That means we can cancel it out!
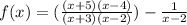
In this simplified version of the fraction, we can technically define f(-1), but in the original version, since it's not defined there is a removable discontinuity at x=-1, meaning there is no vertical asymptote, but the function is still not defined at f(-1), and there will be a hole at that point.