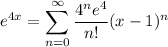Answer:
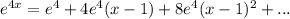
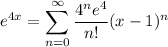
Explanation:
Taylor series expansions of f(x) at the point x = a
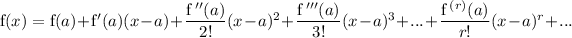
This expansion is valid only if
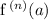 exists and is finite for all
exists and is finite for all
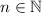 , and for values of x for which the infinite series converges.
, and for values of x for which the infinite series converges.
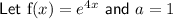
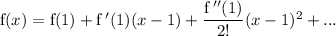
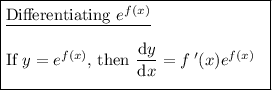



Substituting the values in the series expansion gives:
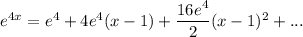
Factoring out e⁴:
![e^(4x)=e^4\left[1+4(x-1)+8}(x-1)^2+...\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/gsc7j1smmmaudcbcvroibuxtqbbumg3kwm.png)
Taylor Series summation notation:
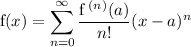
Therefore: