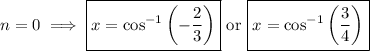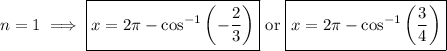Recall the Pythagorean identity,
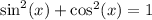
Use it to rewrite the equation in terms of cos only.
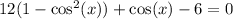
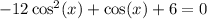
Factorize the left side.
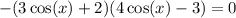
Solve the two cases for
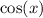 .
.
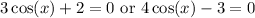
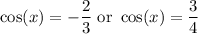
From the first equation, we get one family of solutions:
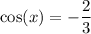
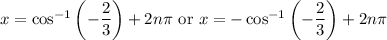
From the second equation, we get another family:
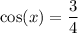
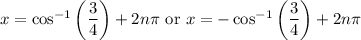
where
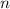 is an integer.
is an integer.
We get solutions in the given domain for