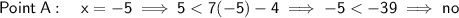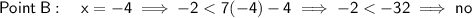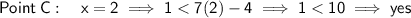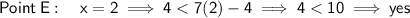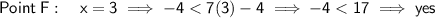Question

100 POINTS PLEASE HELP!!!

The coordinate plane below represents a community. Points A through F are houses in the community.

graph of coordinate plane. Point A is at negative 5, 5. Point B is at negative 4, negative 2. Point C is at 2, 1. Point D is at negative 2, 4. Point E is at 2, 4. Point F is at 3, negative 4.

Part A: Using the graph above, create a system of inequalities that only contains points C and F in the overlapping shaded regions. Explain how the lines will be graphed and shaded on the coordinate grid above. (7 points)

Part B: Explain how to verify that the points C and F are solutions to the system of inequalities created in Part A. (5 points)

Part C: Erica wants to live in the area defined by y < 7x − 4. Explain how you can identify the houses in which Erica is interested in living. (2 points)

Answer 1

`\sf A) \quad \begin{cases}\sf y > -5x+5\\\sf y < -5x+12\end{cases}`

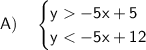
B) see below

C) points C, E and F

Explanation:

Given points:

• A = (-5, 5)
• B = (-4, -2)
• C = (2, 1)
• D = (-2, 4)
• E = (2, 4)
• F = (3, -4)

Part A

A system of inequalities is a set of two or more inequalities in one or more variables.

To create a system of inequalities that only contains C and F in the overlapping shaded region, create a linear equation where points C, F and E are to the right of the line and a linear equation where points C, F, A, B and D are to the left of the line.

The easiest way to do this is to find the slope of the line that passes through points C and F, then add values to move the lines either side of the points.

`\sf slope\:(m)=(change\:in\:y)/(change\:in\:x)=(y_F-y_C)/(x_F-x_C)=(-4-1)/(3-2)=-5`

Therefore:

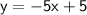`\sf y = -5x + 5` → points C, F and E are to the right of the line.

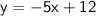`\sf y=-5x+12` → points C, F, A, B and D are the left of the line.

Therefore, the system of inequalities that only contains points C and F in the overlapping shaded regions is:

`\begin{cases}\sf y > -5x+5\\\sf y < -5x+12\end{cases}`

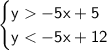
To graph the system of inequalities:

• Plot 2 points on each of the lines.
• Draw a dashed line through each pairs of points.
• Shade the intersected region that is above the line y > -5x + 5 and below the line y < -5x + 12.

Part B

To verify that the points C and F are solutions to the system of inequalities created in Part A, substitute the x-values of both points into the system of inequalities. If the y-values satisfy both inequalities, then the points are solutions to the system.

Point C (2, 1)

`\implies \sf x=2 \implies 1 > -5(2)+5 \implies 1 > -5\quad verified`

`\implies \sf x=2 \implies 1 < -5(2)+12\implies 1 < 2 \quad verified`

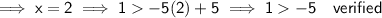
Point F (3, -4)

`\implies \sf x=3 \implies -4 > -5(3)+5 \implies -4 > -10\quad verified`

`\implies \sf x=3 \implies -4 < -5(3)+12\implies -4 < -3 \quad verified`

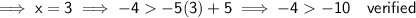
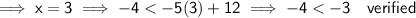
Part C

Method 1

Graph the line y = 7x - 4 (making the line dashed since it is y < 7x - 4).

Shade below the dashed line.

Points that are contained in the shaded region are the houses in which Erica is interested in living: points C, E and F.

Method 2

Substitute the x-value of each point into the given inequality y < 7x - 4.

Any point where the y-value satisfies the inequality is a house that Erica is interested in living.

`\sf Point\: A: \quad x=-5 \implies 5 < 7(-5)-4 \implies -5 < -39 \implies no`

`\sf Point\: B: \quad x=-4 \implies -2 < 7(-4)-4 \implies -2 < -32 \implies no`

`\sf Point\: C: \quad x=2 \implies 1 < 7(2)-4 \implies 1 < 10 \implies yes`

`\sf Point\: D: \quad x=-2 \implies 4 < 7(-2)-4 \implies 4 < -18 \implies no`

`\sf Point\: E: \quad x=2 \implies 4 < 7(2)-4 \implies 4 < 10 \implies yes`

`\sf Point\: F: \quad x=3 \implies -4 < 7(3)-4 \implies -4 < 17 \implies yes`