Question

PLS HELP

Which functions have a range of {y e R-00 < y < 00}?
O f(x)
2x+3
Of(x) = x - 8
O f(x) = x² + 7x - 9
O f(x) = -4x + 11
O f(x) = -(x + 1)² - 4
=

Answer 1

`\displaystyle{1.) \ \ f(x) = (2)/(3)x-8}\\\\\displaystyle{2.) \ \ f(x) = -4x+11}`

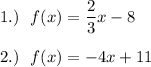
Explanation:

What is Range?

- Range is a set of all y-values in a set of coordinate points.

Consider This:

A linear equation or function always have range equal to set of real number because you can substitute f(x) as any numbers and you'll still be able to solve for x-variable.

An quadratic equation or function may have range equal to set of positive real number or negative real number depending whether if the coefficient of x² is in positive or negative but consider this:

Suppose we have f(x) = x², f(x) cannot be negative number because that'd make the equation not real. Therefore, a quadratic function does not have
`\displaystyle{\mathbb{R}}` range.

For an exponential function, it's same as quadratic equation. It depends whether if a base is in negative or positive. You can consider like this:

Suppose we have
`\displaystyle{f(x)=2^x}`, f(x) cannot be negative number because there are no x-values that make the equation true. Therefore, an exponential function does not have
`\displaystyle{\mathbb{R}}` range as well.