Question

NO LINKS!! Please help me with this problem​

Answer 1

`{\qquad\qquad\huge\underline{{\sf Answer}}}`

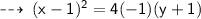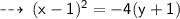
The given vertex and Focus are of a vertical parabola having an opening downward as the focus is in downward direction as the vertex.

Focus of the parabola can be written as :

`\qquad \sf  \dashrightarrow \: (h ,k+ a )`

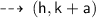
where, h and k are coordinates of vertex

so,

• k + a = -2

• -1 + a = -2

• a = -1

So, the equation of parabola can be written as :

`\qquad \sf  \dashrightarrow \: (x - h) {}^(2) = 4a(y - k)`

plug in the values ~

`\qquad \sf  \dashrightarrow \: (x - 1) {}^(2) = 4(- 1)(y + 1) {}^{}`

`\qquad \sf  \dashrightarrow \: (x - 1) {}^(2) = - 4(y + 1)`

Answer 2

`(x-1)^2=-4(y+1)`

Explanation:

Standard form of a parabola with a vertical axis of symmetry:

`(x-h)^2=4p(y-k) \quad \textsf{where}\:p\\eq 0`

• Vertex = (h, k)
• Focus = (h, k+p)
• Directrix: y = (k-p)
• Axis of symmetry: h = k
• If p > 0, the parabola opens upwards, and if p < 0, the parabola opens downwards.

Given:

• vertex = (1, -1)
• focus = (1, -2)

Comparing with the formulas:

⇒ h = 1

⇒ k = -1

⇒ k + p = -2 ⇒ -1 + p = -2 ⇒ p = -1

Substituting the values into the formula:

`\implies (x-1)^2=4(-1)(y-(-1))`

`\implies (x-1)^2=-4(y+1)`