Question

AB=
BC=
Help me please!! Asap thanks so much

Answer 1

5 and 5

Explanation:

`AB = BC =√((4-0)^2+(3-0)^2)=5`

Answer 2

AB = 5

BC = 5

Explanation:

The formula to find the distance between two points is:
`√((x_2-x_1)^2 +(y_2-y_1)^2)`

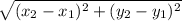
AB: 5

The two points are A(-4,0) and B(0,3).

In the formula, it will be expressed as:

`√((0-(-4))^2+(3-0)^2)`

-->
`√(4^2+3^2)` .

-->
`√(16+9)`

-->
`√(25)`

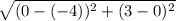
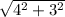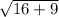
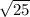
--> 5

BC: 5

The two points are: B(0,3) and C(4,0)

In the formula, it will be expressed as:

`√((4-0)^2+(0-3)^2)`

-->
`√((4)^2 + (-3)^2)`

-->
`√(16 + 9)`

-->
`√(25)`

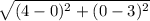
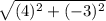
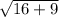
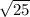
--> 5

So both AB and BC is 5.