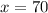Answer:
x=70, y=55
Explanation:
Since the angle "y" and 2x-15 form a straight line, that means the sum of the angles, must be 180 degrees.
So using this we can derive the equation:

The next thing you need to know is that the sum of interior angles of a triangle is 180 degrees, so if we add all the angles, we should get 180.
So using these we can derive the equation:

So, in this case we simply have a systems of equations. We can solve this by solving for x in the second equation (sum of interior angles), and plug that into the first equation.
Original Equation:
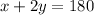
Subtract 2y from both sides
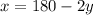
Now let's plug this into the first equation

Plug in 180-2y as x
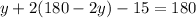
Distribute the 2

Combine like terms
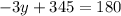
Subtract 345 from both sides
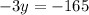
Divide both sides by -3

So we can plug this into either equation to solve for x

Substitute in 55 as y
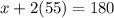
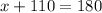
Subtract 110 from both sides