Question

solve the following system {y=x^2-3 and {y=3x-3 graphically and algebraicallyPLEASE HELP ME IM BEGGING

Answer 1

There are two solutions:
x = 0, y = -3 Point (0, -3)
x = 3, y = -6 Point (3, 6)

The solutions are at the intersections of the two individual graphs corresponding to each of the two equations (see attached figure)

Explanation:

Use a graphing calculator or tool to plot each equation. The point of intersection of the two is the solution to the system of equations. See attached image

Algebraically

The first equation must be equal to the second equation for a unique value of y and x


`y = x^2 - 3 = 3x -3\\x^2 - 3 = 3x - 3`

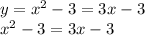
Subtract 3x - 3 from both sides giving

`x^2 - 3 - (3x -3) = 0\\x^2 -3 -3x + 3 = 0\\x^2 - 3x = 0\\`

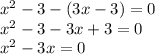
Factoring out x we get

`x(x-3) = 0`

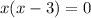
This means that x = 0 and also
x -3 = 0, or x = 3

Substituting for x = 0 in y = 3x-3 gives
y = 3.0 - 3 = -3
So x= 0, y = -3 is one solution (0,-3)

Substituting for x = 3 in the same equation gives
y = 3(3) - 3 = 6
So x = 3, y = 6 is another solution (3, 6)