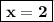Answer:
Vertex (2 , -25)
Axis of symmetry: x = 2
Explanation:
Vertex of parabola:
The vertex is the highest point if the parabola open downwards and the lowest point if the parabola opens upward.
f(x) = (x - 2)² - 25
The given quadratic function is in vertex form.
f(x) = a(x - h)² + k
Here, (h , k) is the vertex of the parabola.
h = 2 ; k = -25

Axis of symmetry:
The axis of symmetry is the vertical line that divides the parabola into two equal halves and it passes through the vertex of the parabola.
Axis of symmetry: x = h