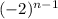Answer:
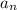 = 3
= 3
Explanation:
there is a common ratio between consecutive terms , that is
- 6 ÷ 3 = 12 ÷ - 6 = - 24 ÷ 12 = 48 ÷ - 24 = - 2
this indicates the sequence is arithmetic with explicit rule
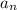 = a₁
= a₁
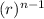
where a₁ is the first term and r the common ratio
here a₁ = 3 and r = - 2 , then
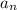 = 3
= 3