Question

Help with these two questions please !!

Answer 1

1. (x + 8)(x + 3)

2. (x - 9)²

Explanation:

Given trinomials:

1.
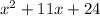
`x^2+11x+24`

2.
`x^2-18x+81`

..................................................................................................................................................

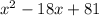
When factoring trinomials of the form ax² + bx + c:

• Multiply the leading coefficient and the last term.
• Find the product factors that add up to give you the coefficient of the middle term.
• Rewrite the polynomial with those factors replacing the middle term.

..................................................................................................................................................

1) x² + 11x + 24

Step 1: Multiply the leading coefficient (1) and the last term (24).

`\implies 1 * 24 = \boxed{24}`

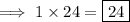
Step 2: Find the product factors that sum up to the middle term's coefficient (11).

`\begin{array} c \cline{1-2} \sf Factors\:of\:24 & \sf Sum\:of\:factors\\\cline{1-2} 1, 24\ \| -1, -24 & 25\ \| -25 \\\cline{1-2} 2, 12\ \| -2, -12 & 14\ \| -14 \\ \cline{1-2} 3, 8\ \| -3, -8 & 11\ \| -11 \\\cline{1-2} 4, 6 \ \| -4, -6 & 10\ \| -10 \\\cline{1-2}\end{array}`

`\implies 3x+8x=11x`

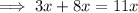
Step 3: Rewrite the polynomial with those factors, replacing the middle term.

`\implies x^2+3x+8x+24`

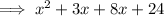
Step 4: Factor by grouping.

`\implies \overbrace{(x^2+3x)}^x+\overbrace{(8x+24)}^8\ \ \textsf{[ Factor out $x$ and $8$. ]}`

`\implies x\overbrace{(x+3)}^{\textsf {Factor out}}+8(x+3)`

`\implies \boxed{(x+8)(x+3)}`

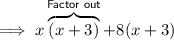
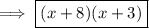
The factored form of the given trinomial is
`(x+8)(x+3)`.

..................................................................................................................................................

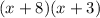2) x² - 18x + 81

Step 1: Multiply the leading coefficient (1) and the last term (81).

`\implies 1 * 81 = \boxed{81}`

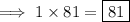
Step 2: Find the product factors that sum up to the middle term's coefficient (-18).

`\begin{array}\cline{1-2} \sf Factors\:of\:81 & \sf Sum\:of\:factors\\\cline{1-2} 1, 81\ \| -1, -81 & 81\ \| -81 \\\cline{1-2} 3, 27\ \| -3, -27 & 30\ \| -30 \\ \cline{1-2} 9, 9\ \| -9, -9 & 18\ \| -18 \\\cline{1-2}\end{array}`

`\implies (-9x)+(-9x)=-18x`

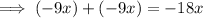
Step 3: Rewrite the polynomial with those factors, replacing the middle term.

`\implies x^2-9x-9x+81`

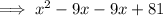
Step 4: Factor by grouping.

`\implies \overbrace{(x^2-9x)}^x+\overbrace{(-9x+81)}^(-9)\ \ \textsf{[ Factor out $x$ and $-9$. ]}`

`\implies x\overbrace{(x-9)}^{\textsf {Factor out}}-9(x-9)`

`\implies (x-9)(x-9)`

`\implies \boxed{(x-9)^2}`

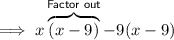
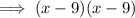
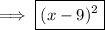
The factored form of the given trinomial is
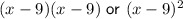`(x-9)(x-9)\ \textsf{or}\ (x-9)^2`.