Question

2. Find rectangular coordinates for the point (6, 240°).

Answer 1

(-3, -3√3)

Step-by-step explanation:

To convert from polar coordinate to rectangular coordinate, first you have to know these two equations:

`\displaystyle{x=r\cos \theta}\\\displaystyle{y=r\sin \theta}`

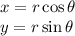
We know that (x,y) is in rectangular coordinate form while (r,θ) is in polar coordinate form.

Therefore, substitute r = 6 and θ = 240° in both equations:

`\displaystyle{x=6\cos 240^(\circ)}\\\displaystyle{y=6\sin 240^(\circ)}`

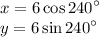
After evaluating, you'll get:

`\displaystyle{x=-3}\\\displaystye{y=-3√(3)}`

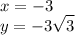
Therefore, substitute x and y in rectangular coordinate form - hence, the answer is (-3, -3√3)