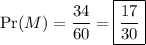Question

6. a. Sixty students in a class took an examination in Physics and Mathematics. If 17 of them passed Physics only, 25 passed in both Physics and Mathematics and 9 of them failed in both subjects, find i. the number of students who passed in Physics ii. the probability of selecting a student who passed in Mathematics 17​

Answer 1

Let
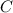`C` be the set of all students in the classroom.

Let
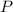`P` and
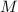`M` be the sets of students that pass physics and math, respectively.

We're given

`n(C) = 60`

`n(P \cap M') = 17`

`n(P \cap M) = 25`

`n((P \cup M)') = n(P' \cap M') = 9`

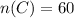
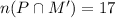
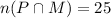
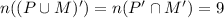
i. We can split up
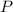`P` into subsets of students that pass both physics and math
`(P\cap M)` and those that pass only physics
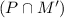`(P\cap M')`. These sets are disjoint, so

`n(P) = n(P\cap M) + n(P\cap M') = 25 + 17 = \boxed{42}`

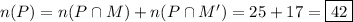
ii. 9 students fails both subjects, so we find

`n(C) = n(P\cup M) + n(P\cup M)' \implies n(P\cup M) = 60 - 9 = 51`

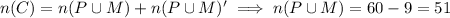
By the inclusion/exclusion principle,

`n(P\cup M) = n(P) + n(M) - n(P\cap M)`

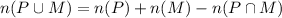
Using the result from part (i), we have

`n(M) = 51 - 42 + 25 = 34`

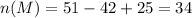
and so the probability of selecting a student from this set is

`\mathrm{Pr}(M) = (34)/(60) = \boxed{(17)/(30)}`