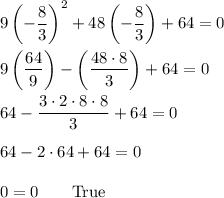Question

Which explains how to show that

X=-8/3
is a root of
9×^2+48×+64=0?

a. Graph
9x^2 + 48x + 64 = 0
to show that
x=-8/3
is where the parabola crosses the y axis.

b. Graph
9x^2 + 48x +64 = 0
to show that the parabola's vertex is just above the value
x=-8/3

c. Substitute
x=-8/3
back into
9x^2 + 48x + 64 =0
and simplify to show that a true statement
results.

d. Substitute
x=-8/3
back into
9x^2 + 48x + 64 = 0
and simplify to show the values of
a
c
remain perfect squares.

Answer 1

c. Substitute

Explanation:

A graph of the function on the left shows the parabola touches the x-axis at x = -8/3. That is, the vertex is on the x-axis. It crosses the y-axis at y = 64.

Show a value is a root

A given solution to an equation can be verified by substituting that value into the equation an showing the result is a true statement. Here, the value x=-8/3 is a root of the given equation because that value makes the equation true.

`9\left(-(8)/(3)\right)^2+48\left(-(8)/(3)\right)+64=0\\\\9\left((64)/(9)\right)-\left((48\cdot8)/(3)\right)+64=0\\\\64-(3\cdot2\cdot8\cdot8)/(3)+64=0\\\\64-2\cdot64+64=0\\\\0=0\qquad\text{True}`