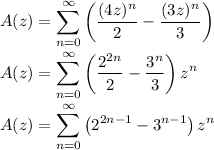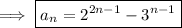Question

Find the general term of sequence defined by these conditions.


`\displaystyle \large{a_1 = 1 \: ,a_2 = 5, \: a_(n + 2) - 7a_(n + 1) + 12a_n = 0}`
Please show your work. Thanks!
Topic: Recurrence Relation​

Answer 1

`\displaystyle a_(n) = (2)^(2n -1) - (3) ^(n-1 )`

Explanation:

we want to figure out the general term of the following recurrence relation

`\displaystyle \rm a_(n + 2) - 7a_(n + 1) + 12a_n = 0 \: \: where : \: \:a_1 = 1 \: ,a_2 = 5,`

we are given a linear homogeneous recurrence relation which degree is 2. In order to find the general term ,we need to make it a characteristic equation i.e

• 
  `{x}^(n) = c_(1) {x}^(n - 1) + c_(2) {x}^(n - 2) + c_(3) {x}^(n -3 ) { \dots} + c_(k) {x}^(n - k)`

the steps for solving a linear homogeneous recurrence relation are as follows:

1. Create the characteristic equation by moving every term to the left-hand side, set equal to zero.
2. Solve the polynomial by factoring or the quadratic formula.
3. Determine the form for each solution: distinct roots, repeated roots, or complex roots.
4. Use initial conditions to find coefficients using systems of equations or matrices.

Step-1:Create the characteristic equation

`{x}^(2) - 7x+ 12= 0`

Step-2:Solve the polynomial by factoring

factor the quadratic:

`( {x}^{} - 4)(x - 3) = 0`

solve for x:

`x = \rm 4 \:and \: 3`

Step-3:Determine the form for each solution

since we've two distinct roots,we'd utilize the following formula:

`\displaystyle a_(n) = c_(1) {x} _(1) ^(n ) + c_(2) {x} _(2) ^(n )`

so substitute the roots we got:

`\displaystyle a_(n) = c_(1) (4)^(n ) + c_(2) (3) ^(n )`

Step-4:Use initial conditions to find coefficients using systems of equations

create the system of equation:

`\begin{cases}\displaystyle 4c_(1) +3 c_(2) = 1 \\ 16c_(1) + 9c_(2) = 5\end{cases}`

solve the system of equation which yields:

`\displaystyle c_(1) = (1)/(2) \\ c_(2) = - (1)/(3)`

finally substitute:

`\displaystyle a_(n) = (1)/(2) (4)^(n ) - (1)/(3) (3) ^(n )`

`\displaystyle \boxed{ a_(n) = (2)^(2n-1 ) - (3) ^(n -1)}`

and we're done!

Answer 2

Consider the generating function of the sequence
`a_n`, defined by

`A(z) = \displaystyle \sum_(n=0)^\infty a_nz^n = a_0 + a_1z + a_2z^2 + \cdots`

(this is also known as the Z-transform of
`a_n`)

While the given sequence isn't exactly defined for n = 0, we can use the recurrence to extend it to cover this case. For n = 0, we get

`a_2 - 7a_1 + 12a_0 = 0 \implies a_0 = -\frac16`

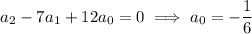
Since for all n ∈ {0, 1, 2, …} we have that

`a_(n+2)-7a_(n+1)+12a_n=0`

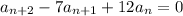
Multiplying both sides by
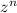`z^n` and summing over all n gives the relation

`\displaystyle \sum_(n=0)^\infty a_(n+2)z^n - 7 \sum_(n=0)^\infty a_(n+1)z^n + 12 \sum_(n=0)^\infty a_nz^n = 0`

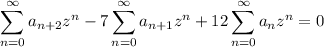
Manipulate the first two series to get them in terms of A(z) :

`\displaystyle \sum_(n=0)^\infty a_(n+2)z^n = \frac1{z^2}\sum_(n=0)^\infty a_(n+2)z^(n+2) \\\\ \sum_(n=0)^\infty a_(n+2)z^n = \frac1{z^2} \sum_(n=2)^\infty a_nz^n \\\\ \sum_(n=0)^\infty a_(n+2)z^n = \frac1{z^2}\left(\sum_(n=0)^\infty a_nz^n - a_0 - a_1z\right) \\\\ \sum_(n=0)^\infty a_(n+2)z^n = (A(z)-\frac16-z)/(z^2)`

and

`\displaystyle \sum_(n=0)^\infty a_(n+1)z^n = \frac1z \sum_(n=0)^\infty a_(n+1)z^(n+1) \\\\ \sum_(n=0)^\infty a_(n+1)z^n = \frac1z\sum_(n=1)^\infty a_nz^n \\\\ \sum_(n=0)^\infty a_(n+1)z^n = \frac1z\left(\sum_(n=0)^\infty a_nz^n - a_0\right) \\\\ \sum_(n=0)^\infty a_(n+1)z^n = (A(z)-\frac16)/(z)`

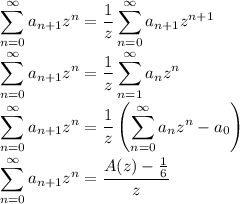
The third series is simply A(z).

Solve this new recurrence for A(z) :

`\displaystyle (A(z)-\frac16-z)/(z^2) - (7A(z)-\frac76)/(z) + 12 A(z) = 0 \\\\ (A(z))/(z^2)-(7A(z))/(z) + 12A(z) = \frac1{6z^2}+\frac1z-\frac7{6z} \\\\ (A(z)-7zA(z)+12z^2A(z))/(z^2) = (1-z)/(6z^2) \\\\ (1-7z+12z^2)/(z^2)A(z) = (1-z)/(6z^2) \\\\ A(z) = (1-z)/(6(1-7z+12z^2))`

The next step is to find the power series expansion for A(z) to recover
`a_n`. Factorize the denominator, then decompose A(z) into partial fractions:

`1-7z+12z^2 = (1-3z)(1-4z)`

`\displaystyle (1-z)/((1-3z)(1-4z)) = \frac a{1-3z} + \frac b{1-4z} \\\\ 1-z = a(1-4z) + b(1-3z) \\\\ 1-z = a+b + (-4a-3b)z \\\\ \implies a=-2, b=3`

`\implies \displaystyle A(z) = \frac16\left(\frac3{1-4z} - \frac2{1-3z}\right)`

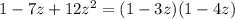
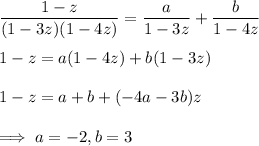
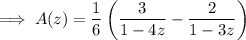
Recall that for |z| < 1, we have

`\displaystyle \sum_(n=0)^\infty z^n = \frac1{1-z}`

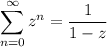
Then if |4z| < 1, we can write A(z) as the sum of two convergent geometric series,

`\displaystyle A(z) = \frac12 \sum_(n=0)^\infty (4z)^n - \frac13 \sum_(n=0)^\infty (3z)^n`

and some rewriting to put this in the canonical G.F. form lets us easily pick out
`a_n`.

`\displaystyle A(z) = \sum_(n=0)^\infty \left(\frac{(4z)^n}2 - \frac{(3z)^n}3 \right) \\\\ A(z) = \sum_(n=0)^\infty \left(\frac{2^(2n)}2 - \frac{3^n}3\right)z^n \\\\ A(z) = \sum_(n=0)^\infty \left(2^(2n-1) - 3^(n-1)\right)z^n`

`\implies \boxed{a_n = 2^(2n-1) - 3^(n-1)}`