Answer:
Choice b.
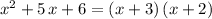 .
.
Explanation:
The highest power of the variable
 in this polynomial is
in this polynomial is
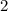 . In other words, this polynomial is quadratic.
. In other words, this polynomial is quadratic.
It is thus possible to apply the quadratic formula to find the "roots" of this polynomial. (A root of a polynomial is a value of the variable that would set the polynomial to
 .)
.)
After finding these roots, it would be possible to factorize this polynomial using the Factor Theorem.
Apply the quadratic formula to find the two roots that would set this quadratic polynomial to
 . The discriminant of this polynomial is
. The discriminant of this polynomial is
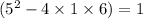 .
.
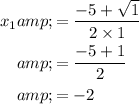 .
.
Similarly:
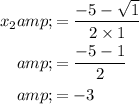 .
.
By the Factor Theorem, if
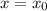 is a root of a polynomial, then
is a root of a polynomial, then
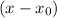 would be a factor of that polynomial. Note the minus sign between
would be a factor of that polynomial. Note the minus sign between
 and
and
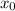 .
.
- The root
 corresponds to the factor
corresponds to the factor
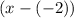 , which simplifies to
, which simplifies to
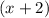 .
. - The root
 corresponds to the factor
corresponds to the factor
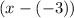 , which simplifies to
, which simplifies to
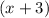 .
.
Verify that
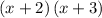 indeed expands to the original polynomial:
indeed expands to the original polynomial:
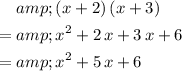 .
.