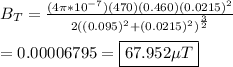Hi there!
a)
Let's use Biot-Savart's law to derive an expression for the magnetic field produced by ONE loop.
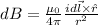
dB = Differential Magnetic field element
μ₀ = Permeability of free space (4π × 10⁻⁷ Tm/A)
R = radius of loop (2.15 cm = 0.0215 m)
i = Current in loop (0.460 A)
For a circular coil, the radius vector and the differential length vector are ALWAYS perpendicular. So, for their cross-product, since sin(90) = 1, we can disregard it.

Now, let's write the integral, replacing 'dl' with 'ds' for an arc length:
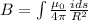
Taking out constants from the integral:
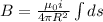
Since we are integrating around an entire circle, we are integrating from 0 to 2π.
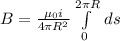
Evaluate:
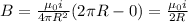
Plugging in our givens to solve for the magnetic field strength of one loop:
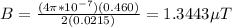
Multiply by the number of loops to find the total magnetic field:

b)
Now, we have an additional component of the magnetic field. Let's use Biot-Savart's Law again:
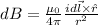
In this case, we cannot disregard the cross-product. Using the angle between the differential length and radius vector 'θ' (in the diagram), we can represent the cross-product as cosθ. However, this would make integrating difficult. Using a right triangle, we can use the angle formed at the top 'φ', and represent this as sinφ.

Using the diagram, if 'z' is the point's height from the center:
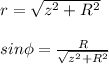
Substituting this into our expression:
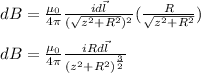
Now, the only thing that isn't constant is the differential length (replace with ds). We will integrate along the entire circle again:
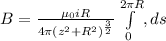
Evaluate:
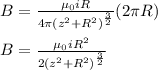
Multiplying by the number of loops:
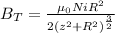
Plug in the given values: