Question

Need help with number 3 inequalities with variables on both sides

Answer 1

Answer:
`x \leq 2`

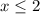
Step-by-step explanation: Given
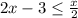`2x - 3 \leq (x)/(2)`, we multiply 2 by both sides to cancel out the 2 in the denominator (multiplying by a number in a fraction turns it into 1, and since the denominator is one, it is the same as saying the number [or variable] on the numerator by itself.)

We then get
`4x - 6 \leq x`.

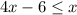Adding 6 to both sides, we get
`4x \leq x + 6`.

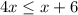Subtracting x from both sides, we get
`3x \leq 6`

Dividing by 3 from both sides, we get
`x \leq 2`

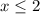
Hope this helped!

Answer 2

x ≤ 2

Explanation:

We are given the inequality:

`\displaystyle{2x-3 \leq (x)/(2)}`

First, get rid of the denominator by multiplying both sides by 2:

`\displaystyle{2x\cdot 2-3\cdot 2 \leq (x)/(2)\cdot 2}\\\\\displaystyle{4x-6 \leq x}`

Add both sides by 6 then subtract both sides by x:

`\displaystyle{4x-6+6 \leq x+6}\\\\\displaystyle{4x \leq x+6}\\\\\displaystyle{4x-x \leq x+6-x}\\\\\displaystyle{4x-x \leq 6}\\\\\displaystyle{3x \leq 6}`

Then divide both sides by 3:

`\displaystyle{(3x)/(3) \leq (6)/(3)}\\\\\displaystyle{x \leq 2}`

Therefore, the answer is x ≤ 2