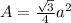Question

What is the area of an equilateral triangle having side 'a' units?
​

Answer 1

`A=(√(3))/(4)a^2`

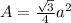
Explanation:

Since an equilateral has all of the sides equal, we can find the height of triangle using:
`a^2+b^2=c^2`. I attached a diagram which should explain how I got the dimensions of the three sides. Using the information from the diagram we get the equation:

`h^2+((a)/(2))^2=a^2`

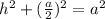
Subtract a^2 from both sides

`h^2=a^2-((a)/(2))^2`

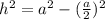
Take the square root of both sides

`h = \sqrt{a^2-((a)/(2))^2}`

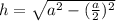
If you know the area of a triangle, it's:
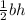`(1)/(2)bh`. In this case the base=a, and the height is what we defined above. Using this we get:

`A = (a)/(2)*\sqrt{a^2-((a)/(2))^2}`

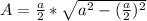
We can distribute the exponent over the division to get:

`A = (a)/(2)*\sqrt{a^2-((a^2)/(4))`

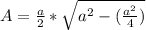
Now we can rewrite a^2 as 4a^2/4

`A = (a)/(2)*\sqrt{(4a^2)/(4)-((a^2)/(4))`

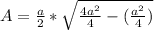
Now add the two fractions:

`A = (a)/(2)*\sqrt{(3a^2)/(4)`

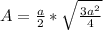
We can distribute the square root the division just like how we distributed the exponent 2, since the square root can be expressed as an exponent (1/2)

`A = (a)/(2)*(√(3a^2))/(√(4))`

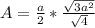
There's a radical identity that states:
`\sqrt[n]{a} * \sqrt[n]{b} = \sqrt[n]{a*b}`. We can use this to rewrite one radical as multiple radicals to simplify it:

`A = (a)/(2)*(√(a^2)*√(3))/(2)`

Simplify:

`A = (a)/(2)*(a*√(3))/(2)`

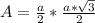
Now multiply the two fractions

`A = (a^2*√(3))/(4)`

This is the formula for the area of an equilateral triangle, but it is also often written as:

`A=(√(3))/(4)a^2`