Question

A plank of length L=2.200 m and mass M=4.00 kg is suspended horizontally by a thin cable at one end and to a pivot on a wall at the other end as shown. The cable is attached at a height H=1.70 m above the pivot and the plank's CM is located a distance d=0.700 m from the pivot.

Calculate the tension in the cable.

Answer 1

Hello!

Let's begin by doing a summation of torques, placing the pivot point at the attachment point of the rod to the wall.

`\Sigma \tau = 0`

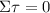
We have two torques acting on the rod:
- Force of gravity at the center of mass (d = 0.700 m)

- VERTICAL component of the tension at a distance of 'L' (L = 2.200 m)

Both of these act in opposite directions. Let's use the equation for torque:

`\tau = r * F`

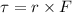
Doing the summation using their respective lever arms:

`0 = L Tsin\theta - dF_g`

`dF_g = LTsin\theta`

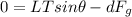
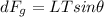
Our unknown is 'theta' - the angle the string forms with the rod. Let's use right triangle trig to solve:

`tan\theta = (H)/(L)\\\\tan^(-1)((H)/(L)) = \theta\\\\tan^(-1)((1.70)/(2.200)) = 37.69^o`

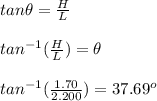
Now, let's solve for 'T'.

`T = (dMg)/(Lsin\theta)`

Plugging in the values:

`T = ((0.700)(4.00)(9.8))/((2.200)sin(37.69)) = \boxed{20.399 N}`