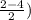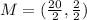Question

Use the information provided to write the general conic form equation of the circle: Ends of a diameter: (11, -2) and (9, 4)

Answer 1

The equation for a circle is:

`(x-a)^(2) + (y-b)^(2) + = r^(2)`

Where (a,b) is the circle's center and r is the circle's radius.

First, we can find the center point of the circle. Because the two points from the problem are the endpoints of a diameter, the midpoint of the line segment is the center point of the circle.

The formula to find the mid-point of a line segment giving the two endpoints is:

M =
`((x_(1) + x_(2) )/(2)`,
`(y_(1) + y_(2) )/(y) )`

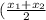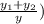
Where M is the midpoint and the given points are:

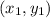`(x_(1), y_(1) )` and
`(x_(2) , y_(2))`

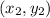
Substituting the values from the two points in the problem gives:

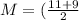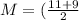`M = ((11+9)/(2)`,
`(-2+4)/(2) )`

`M = ((11+9)/(2)`,
`(2-4)/(2))`

`M = ((20)/(2) , (2)/(2))`

`M = (10,1)`