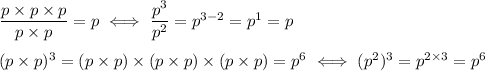Question

This is really hard please help

Answer 1

9514 1404 393

Answer:

(b) p^(m+n)

Explanation:

The rule for exponents is ...

(a^b)(a^c) = a^(b+c)

Here, you have a=p, b=m, c=n, so the product is ...

(p^m)(p^n) = p^(m+n)

_____

Additional comment

I find it useful to remember that an exponent signifies repeated multiplication.

p × p = p² . . . . . the exponent of 2 means p is a factor 2 times in the product

p × p × p = p³ . . . the exponent 3 means p is a factor 3 times in the product

Now, look at what happens when I multiply one of these by the other:

(p×p) × (p×p×p) is a product with p being a factor 2+3 = 5 times

Using exponent notation for the repeated multiplication, this is ...

`p^2* p^3=p^(2+3)=p^5`

__

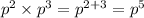
This "repeated multiplication" idea makes it relatively simple to understand other rules of exponents. When we divide, we cancel factors, so the exponents subtract. When we raise to a power, we multiply the number of factors, so the exponents multiply.

`(p* p* p)/(p* p)=p\ \Longleftrightarrow\ (p^3)/(p^2)=p^(3-2)=p^1=p\\\\(p* p)^3=(p* p)*(p* p)*(p* p)=p^6\ \Longleftrightarrow\ (p^2)^3=p^(2*3)=p^6`