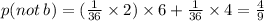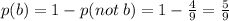Event A:
Pairs that make the sum greater than 8:
(3,6) (4,6) (5,6) (6,6) (4,5) (5,5)
Each of these pairs is equiprobable and which i will be using throughout the exercise:
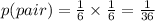

The 2 (2!) is to account for permutations like ( 3 , 6 ) and ( 6 , 3 ) and the 4 are the different combinations that are composed of different numbers.
The 2 (2!) is to account for permutations like ( 3 , 6 ) and ( 6 , 3 ) and the 4 are the different combinations that are composed of different numbers.Whereas combinations like ( 5 , 5 ) cannot be switched in order, so we do not multiply by 2!
Event B
Pairs that yield a sum divisible by 4 or 5: 0,4,5,8,10,12,
(1,3) (2,2) (2,6) (4,4) (5,3) (6,6) (1,4) (2,3) (5,5) (4,6)