a) The z-value associated with 25.0
Z = 1.25
b) proportion of the population is between 20.0 and 25.0 is
Proportion = 0.3944
c) proportion of the population is less than 18.0 is
Proportion = 0.3085
Calculations:
Normal pop has mean of 20.0
standard deviation = 4.0
XNN(20.0, 4.0)
a).
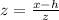
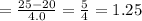
Z = 1.25
b).
The proportion between 20 and 25 is P(20 <x<25.0)
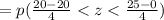
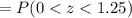
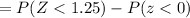
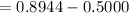
P(20 < x < 25)=0.3944
c).
The proportion value is less than 18 when
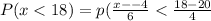
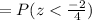
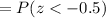
P(x<18) = 0.3085