Answer:
(- 1, - 4 ) and x = - 1
Explanation:
given a parabola in standard form
y = ax² + bx + c ( ax≠ 0 )
then the x- coordinate of the vertex is
x = -
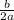
y = x² + 2x - 3 ← is in standard form
with a = 1, b = 2 , then
x = -
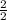 = - 1
= - 1
substitute x = - 1 into the equation for corresponding y- coordinate
y = (- 1)² + 2(- 1) - 3 = 1 - 2 - 3 = - 4
vertex = (- 1, - 4 )
this is an upward opening parabola ( a > 0 )
the axis of symmetry is a vertical line passing through the vertex with equation
x = c ( c is the value of the x- coordinate of the vertex ), then equation is
x = - 1