Question

6. (04.05 MC)

Which Inequality matches the graph? (1 point)

-2x+3y>7
2x+3y <7
-3x+2y>7
3x-2y <7

Answer 1

Answer: Choice D

3x - 2y < 7

=============================================================

Step-by-step explanation:

The dashed boundary line goes through (1, -2) and (3, 1)

Find the slope of this line using the slope formula.

`(x_1,y_1) = (1,-2) \text{ and } (x_2,y_2) = (3,1)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (1 - (-2))/(3 - 1)\\\\m = (1 + 2)/(3 - 1)\\\\m = (3)/(2)\\\\`

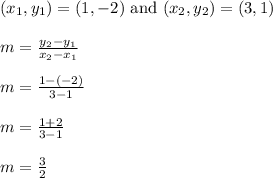
The slope is 3/2 indicating we go up 3 and to the right 2.

--------------

Now use the point-slope template so we can determine the equation of the boundary line.

`y - y_1 = m(x - x_1)\\\\y - (-2) = (3)/(2)(x - 1)\\\\y + 2 = (3)/(2)(x - 1)\\\\2(y+2) = 3(x-1) \ \ \text{ see note1 below}\\\\2y + 4 = 3x - 3\\\\2y - 3x = -3 - 4\\\\-3x+2y = -7\\\\3x-2y = 7 \ \ \text{ see note2 below}\\\\`

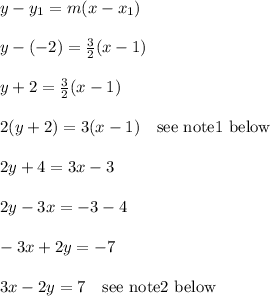
Note1: For this step, I multiplied both sides by 2 to clear out the fraction.

Note2: Multiply both sides by -1 so that the x coefficient is positive

--------------

The key thing to pull away from the previous section is that the boundary line equation is 3x - 2y = 7

The question from here is: "What do we replace the equal sign with?"

We need to pick either < or > since we have a dashed boundary. We won't have an "or equal to" portion.

Let's assume the inequality sign is <

3x - 2y = 7 turns into 3x - 2y < 7

To see if this works, we'll plug in the origin (0,0) to get...

3x - 2y < 7

3(0) - 2(0) < 7

0 < 7

The last inequality above is true, so 3x - 2y < 7 is also true when x = 0 and y = 0. It tells us that the origin is in the shaded region. This matches with what the graph shows.

Therefore, we have confirmed that 3x - 2y < 7 is indeed the case.

You could pick other test points. However the origin is the easiest to work with in my opinion. If the boundary went through the origin, then you'd have to pick another point like (0,1).

If you want to use technology to verify the answer, then Desmos and GeoGebra are two good options to go for. See the screenshots below.