Answer:
(a) none
Explanation:
A "hole" in the graph of f(x) is located at an x-value where the left limit of the function and the right limit are the same finite value, but the function is undefined at that value of x.
Example
The function f(x) = (x -2)/(x -2) can be reduced to the function f(x) = 1, which is defined everywhere. That reduction occurs when the numerator factor (x-2) cancels the same binomial denominator factor. A graph of the original function will be a straight horizontal line with a "hole" at (2, 1).
The attachment shows a graph.
Given Function
The given function can be reduced, but the reduced function remains undefined at x=1/2. Not all of the denominator factors are cancelled there. The function is graphed in the second attachment. At x=1/2, there is a vertical asymptote, not a hole.
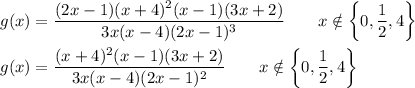
There are no holes in the function's graph.
__
Additional comment
A hole can occur for a variety of reasons. In the graph of a rational function, it will generally be found where numerator and denominator zeros cancel each other completely, and the function can be "reduced" to one that is define at the location of those zeros.
It can also occur in piecewise defined functions, where the pieces are defined on adjoining (half) open intervals. For example:
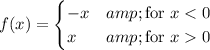
has a hole at (0, 0).