Question

What is the area of the given figure?

10 in.
O 192 units²
O
92.9 units²
O 101.8 units²
O167.2 units2
O
176.7 units2
6 in.
10 in.
9 in.

Answer 1

`\huge\boxed{192\ \text{in}^2}`

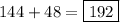
There are three parts to this figure: a rectangle and two triangles that are congruent.

We'll add together the area for each to get the total area.

We'll start by finding the area of the rectangle. We don't know its length, so we need to find the bases of the triangles and add them together.

We know that
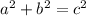`a^2+b^2=c^2`. Substitute and solve for
`a`:

`\begin{aligned}a^2+6^2&=10^2\\a^2+36&=100\\a^2+36-36&=100-36\\a^2&=64\\√(a^2)&=√(64)\\a&=8\end{aligned}`

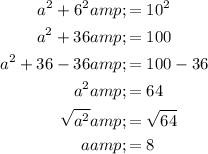
Now, double this to get the total length of the rectangle, which is
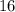`16` inches.

The area of the rectangle is equal to its length times its height:

`16\cdot9=\underline{144}`

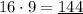
Now, we'll find the area of one of the triangles and double it since they're congruent.

The area of a triangle is one-half of its base times its height, which we then double.

`2\left((1)/(2)\cdot b\cdot h\right)`

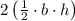
The
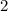`2` and the
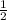`(1)/(2)` cancel each other out.

`b\cdot h`

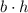
Substitute and solve:

`8\cdot6=\underline{48}`

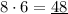
Finally, add the rectangle's area to the two triangles' area.

`144+48=\boxed{192}`