Question

Use any method to solve the equation. If necessary, round to the nearest hundredth.
7x^2-16x=8

Answer 1

The two answers:

2.707778736

0.42206445

Explanation:

Here is the equation:

`{7x}^(2) - 16x = 8`

Take away the 8 from the right hand side, so that we are left with this quadratic equation:

`{7x}^(2) - 16x - 8 = 0`

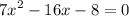
This equation is too complex to solve with the factorizing method, so let's use the quadratic formula, which is as follows:

`x = (-b \pm √(b^2 - 4ac))/(2a)`

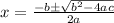
In this equation, a = 7, b = -16, and c = -8. So let's substitute in:

`x = \frac{-( - 16) \pm \sqrt{ { - 16}^(2) - 4 * 7 * - 8}}{2 * 7}`

`x = ( - ( - 16) \pm √(256 + 224) )/(14)`

`x = ( 16 \pm √(480))/(14)`

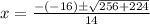
And let's work out the two possible answers:.

2.707778736

0.42206445

Answer 2

Hello,

Answer:

S = { -0,42 ; 2,71 }

Explanation:

7x² - 16x = 8 ⇔ 7x² - 16x - 8 = 0

a = 7 ; b = -16 ; c = -8

Δ = b² - 4ac = (-16)² - 4 × 7 × (-8) = 480 > 0

x₁ = (-b - √Δ)/2a = (16 - √480)/14 ≈ -0,42

x₂ = (-b + √Δ)/2a = (16 + √480)/14 ≈ 2,71