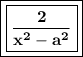- Simplify ⇨ 1/x(x+a) + 1/x(x-a)
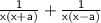
To add or subtract expressions, expand them to make their denominators the same. Least common multiple of
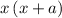 and
and
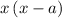 is
is
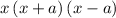 . Multiply
. Multiply
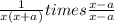 . Multiply
. Multiply
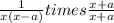 .
.
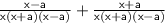
Because
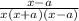 and
and
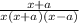 have the same denominator, add them by adding their numerators.
have the same denominator, add them by adding their numerators.
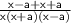
Combine like terms in x-a+x+a.
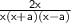
Cancel out x in both the numerator and denominator.
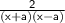
Expand
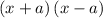 .
.