Answer:
Explanation:
First, you gotta work out the hypotenuse of ABC, which is AC.
To do that, you need to figure out the scale factor between the two right-angled triangles. You can do that for this question because this is a similar shapes question.
12.5/5 = 2.5
The scale factor length between the two triangles is 2.5.
You can use 2.5 now to work out AC, so AC would be 13 x 2.5, which gives 32.5.
Now that you've got the hypotenuse and BC of ABC, you can use Pythagoras's theorem to work out the length of AB
Pythagoras's theorem =
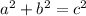
a = BC = 12.5
b = AB = we need to work this out
c = AC (the hypotenuse we just worked out) = 32.5
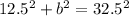 Let's both simplify and rearrange this at the same time so that we have our b on one side.
Let's both simplify and rearrange this at the same time so that we have our b on one side.
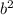 = 1056.25 - 156.25
= 1056.25 - 156.25
b =
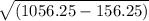
b =
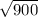
b = AB = 30 We've found b or AB, now we can work out the perimeter of ABC.
Perimeter of ABC = AB + BC + AC
= 30 + 12.5 + 32.5
= 75 Here's the perimeter for ABC.