Question

And the tables represent two linear functions in a system

what solution to the system?

​

Answer 1

The 'x' and 'y' values representing the solution of the system containing the two linear functions are;

x = -14, and y = -54

Explanation:

From the given data table, we have;

The slope of the linear function on the left, 'm', is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

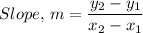
∴ m = (14 - (-22))/(3 - (-6)) = 4

Therefore, the equation in point and slope form we have;

y - 14 = 4·(x - 3)

y = 4·(x - 3) + 14

Similarly for the second linear function on the right, we have;

m = (-3 - (-30))/(3 - (-6)) = 3

Therefore, the equation in point and slope form we have;

y - (-3) = 3·(x - 3)

y = 3·(x - 3) - 3

Equating both 'y' values gives;

4·(x - 3) + 14 = 3·(x - 3) - 3

4·x + 2 = 3·x - 12

4·x - 3·x = x = -12 - 2 = -14

x = -14

y = 4·(x - 3) + 14 = 4 × (-14 - 3) + 14 = - 54

y = -54

Therefore, the solution of the system containing the two linear functions is x = -14, and y = -54