Question

If n is a positive integer, how many 5-tuples of integers from 1 through n can be formed in which the elements of the 5-tuple are written in increasing order but are not necessarily distinct? In other words, how many 5-tuples of integers (h, i, j, k, m) are there with 1 ≤ h ≤ i ≤ j ≤ k ≤ m ≤ n? As in Example 9.6.3, you can represent any ordered 5-tuple of integers (h, i, j, k, m) with 1 ≤ h ≤ i ≤ j ≤ k ≤ m ≤ n as a string of n − 1 vertical bars and 5 crosses, with the position of crosses indicating which 5 integers from 1 to n are included in the 5-tuple. Thus, the number of 5-tuples is the same as the number of strings of n+4 vertical bars and 5 crosses, which is n(n+1)(n+2)(n+3)(n+4) 120​ .

Answer 1

`((n+4)*(n+3)*(n+2)*(n+1)*n)/(120)`

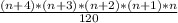
Explanation:

Given

5 tuples implies that:

`n = 5`

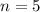
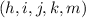`(h,i,j,k,m)` implies that:

`r = 5`

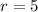
Required

How many 5-tuples of integers
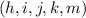`(h, i, j, k,m)` are there such that
`n\ge h\ge i\ge j\ge k\ge m\ge 1`

From the question, the order of the integers h, i, j, k and m does not matter. This implies that, we make use of combination to solve this problem.

Also considering that repetition is allowed: This implies that, a number can be repeated in more than 1 location

So, there are n + 4 items to make selection from

The selection becomes:

`^(n)C_r => ^(n + 4)C_5`

`^(n + 4)C_5 = ((n+4)!)/((n+4-5)!5!)`

`^(n + 4)C_5 = ((n+4)!)/((n-1)!5!)`

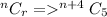
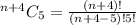
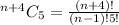
Expand the numerator

`^(n + 4)C_5 = ((n+4)!(n+3)*(n+2)*(n+1)*n*(n-1)!)/((n-1)!5!)`

`^(n + 4)C_5 = ((n+4)*(n+3)*(n+2)*(n+1)*n)/(5!)`

`^(n + 4)C_5 = ((n+4)*(n+3)*(n+2)*(n+1)*n)/(5*4*3*2*1)`

`^(n + 4)C_5 = ((n+4)*(n+3)*(n+2)*(n+1)*n)/(120)`

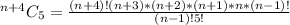
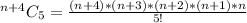
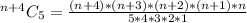
Solved