Question

- Use an appropriate formula to calculate how many terms there are in the sequence

2, 10, 50, ...31250.

*please put full solution

Answer 1

7 terms

Explanation:

There is a common ratio between consecutive terms, that is

r = 10 ÷ 2 = 50 ÷ 10 = 5

This indicates the sequence is geometric with nth term

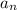`a_(n)` = a₁
`r^(n-1)`

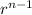
where a₁ is the first term and r the common ratio

Here a₁ = 2 and r = 5, then equating to 31250 and solving for n

2 ×
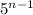`5^(n-1)` = 31250 ( divide both sides by 2 )

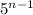`5^(n-1)` = 15625 =
`5^(6)`

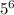
Since bases on both sides are equal, both 5, equate exponents

n - 1 = 6 ( add 1 to both sides )

n = 7

That is there are 7 terms in the sequence