Answer:
a.
 chance you win.
chance you win.
b. The expected value of the game is -$2.08.
Explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
You roll 2 die and if you toss 2 sixes
For each roll, 6 possible values, 1 of which is 6. So the probability of rolling two sixes is:
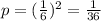
a. What is the chance you win?
 chance you win.
chance you win.
b. What is the expected value of the game?
1/36 probability of winning 100.
35/36 probability of losing 5. So

The expected value of the game is -$2.08.