Question

7

Carly has a bank account with a balance of $3,575. The account pays simple interest at a rate of
4.15%. How long will it take for the account to grow to $7000? Round to the nearest year.

Answer 1

It will take 23 years for the account to grow to $7000.

Explanation:

Simple Interest

The simple interest formula is given by:

`E = P*I*t`

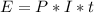
In which E is the amount of interest earned, P is the principal(the initial amount of money), I is the interest rate(yearly, as a decimal) and t is the time.

After t years, the total amount of money is:

`T = E + P`

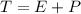
Carly has a bank account with a balance of $3,575.

This means that
`P = 3575`

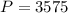
The account pays simple interest at a rate of 4.15%.

This means that
`I = 0.0415`

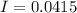
How long will it take for the account to grow to $7000?

`T = 7000`

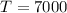
The interest is:

`T = E + P`

`E = T - P = 7000 - 3575 = 3425`

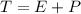
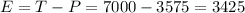
Now we have to find t.

`E = P*I*t`

`3425 = 3575*0.0415*t`

`t = (3425)/(3575*0.0415)`

`t = 23.1`

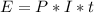
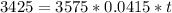
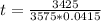
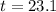
Rounding to the nearest year, it will take 23 years for the account to grow to $7000.