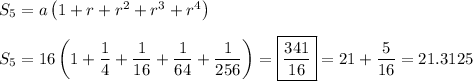Since 64/3 = 21 + 1/3 > 21, I assume S is supposed to be the value of the infinite sum. So we have for some constants a and r (where |r | < 1),
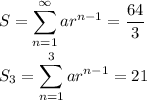
Consider the k-th partial sum of the series,
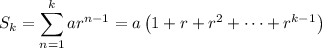
Multiply both sides by r :
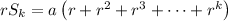
Subtract this from
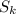 :
:
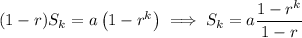
Now as k goes to ∞, the r ᵏ term converges to 0, which leaves us with
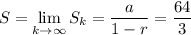
which we can solve for a :

Meanwhile, the 3rd partial sum is given to be
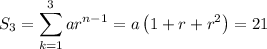
Substitute a into this equation and solve for r :
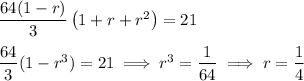
Now solve for a :
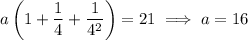
It follows that