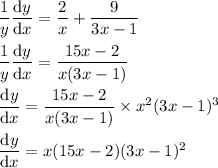Question

How to differentiate ?

Answer 1

Use the power, product, and chain rules:

`y = x^2 (3x-1)^3`

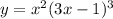
• product rule

`(\mathrm dy)/(\mathrm dx) = (\mathrm d(x^2))/(\mathrm dx)*(3x-1)^3 + x^2*(\mathrm d(3x-1)^3)/(\mathrm dx)`

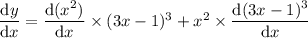
• power rule for the first term, and power/chain rules for the second term:

`(\mathrm dy)/(\mathrm dx) = 2x*(3x-1)^3 + x^2*3(x-1)^2*(\mathrm d(3x-1))/(\mathrm dx)`

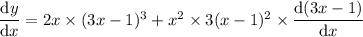
• power rule

`(\mathrm dy)/(\mathrm dx) = 2x*(3x-1)^3 + x^2*3(3x-1)^2*3`

Now simplify.

`(\mathrm dy)/(\mathrm dx) = 2x(3x-1)^3 + 9x^2(3x-1)^2 \\\\ (\mathrm dy)/(\mathrm dx) = x(3x-1)^2 * (2(3x-1) + 9x) \\\\ \boxed{(\mathrm dy)/(\mathrm dx) = x(3x-1)^2(15x-2)}`

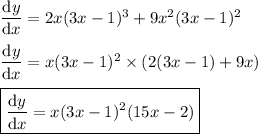
You could also use logarithmic differentiation, which involves taking logarithms of both sides and differentiating with the chain rule.

On the right side, the logarithm of a product can be expanded as a sum of logarithms. Then use other properties of logarithms to simplify

`\ln(y) = \ln\left(x^2(3x-1)^3\right) \\\\ \ln(y) =  \ln\left(x^2\right) + \ln\left((3x-1)^3\right) \\\\ \ln(y) = 2\ln(x) + 3\ln(3x-1)`

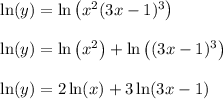
Differentiate both sides and you end up with the same derivative:

`\frac1y(\mathrm dy)/(\mathrm dx) = \frac2x + \frac9{3x-1} \\\\ \frac1y(\mathrm dy)/(\mathrm dx) = (15x-2)/(x(3x-1)) \\\\ (\mathrm dy)/(\mathrm dx) = (15x-2)/(x(3x-1)) * x^2(3x-1)^3 \\\\ (\mathrm dy)/(\mathrm dx) = x(15x-2)(3x-1)^2`